
James Miller G3RUH
In time the program accumulated several other modules, with the mathematics described in interim O.N. articles. When issued for the BBC micro the program acquired the name "PLAN10", and later "PLAN13", and it's been transcribed for several other machines including the IBM-PC and Commodore 64 etc.
In recent years or so my mail has featured more and more queries about tracking matters than was usual. The flavour of these suggests that a new generation of satellite enthusiasts is emerging and are rightly asking the old questions anew.
So for a long while I've been intending to re-publish these routines, but in their most up-to-date embodiment. Hence this pamphlet. I don't intend to provide 100% mathematical details. To do so means essentially writing the whole program out anyway, and references are plentiful.
Old hands will recognise the coding style. Additions include the Sun's position, eclipses, visibility, Sun angle, sub-satellite point, mode switching, date algorithms and direct range-rate calculations for doppler shift.
Almost every publication to do with satellites has information about orbits and their properties. For general reading The Satellite Experimenter's Handbook [2] is unsurpassed, and itself documents several hundred references. Fundamentals of Astrodynamics [3] is a no-nonsense text that's full of insights, and is incredibly cheap.
Models for the Propagation of NORAD Element Sets [4] documents five ways to use a set of keps properly. SGP, the simplest model, runs to 4 pages of higher mathematics just to compute satellite position and velocity. All amateur implementations (i.e. lines 2000-2210 of PROCsatvec) use only the first half page of this, skipping the long term perturbatory effects. Sun's Up [5] is about modelling the Sun's position, and describes applications including illumination and eclipses. 30.6 days Hath September [6] documents date algorithms. The Astronomical Almanac [7] is invaluable for checking calculations; an annual, but useful for many years.
Surprisingly when OSCAR10.BAS was published there were complaints that "filling Oscar News with programs was a waste of space" etc etc. My reply to this myopic view was, and remains:
"The program was designed to be more than a mere listing to be blindly typed in and run. It is a treatise giving all the equations for solving the elliptic orbit and related problems. To do this, as well as provide a tool suitable for immediate use the program was written in a quasi-algebraic style. Variable names were chosen to be meaningful, there are copious comments, and routines are written so that users can adapt them as they wish. However the published arrangement is not the only one. The program is a clear formulation of the general satellite orbit problem, and is sure to provide the interested amateur with several months of absorbing self-training material". Plunder! Enjoy!


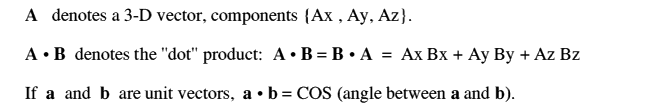
2. Davidoff M.R., Satellite Experimenter's Handbook, 2nd edition, ARRL 1990. ISBN 0-87259-004-6.
3. Bate R., Mueller D. & White J., Fundamentals of Astrodynamics, Dover 1971. ISBN 0-486-60061-0.
4. Hoots F.R. & Roerich R.L., Models for Propagation of NORAD Element Sets, USAF Spacetrack Report No.3, 1988 December.
5. Miller J.R., Sun's Up Part 1, Oscar News, 1984 Dec, No.50 p.2-6; Part 2, 1985 Feb, No.51 p.2-6; "Part 3", 1985 Apr, No.52 p.8-11.
6. Miller J.R., 30.6 days hath September, Oscar News, 1985 Dec, No.56 p.6-9.
7. The Astronomical Almanac 1984, Section C, TSO and USGPO. ISBN 0-11-886919-1
PLAN13 v2.0 SATELLITE PREDICTIONS ----------------------------------- Enter start date (e.g. 1990, 12, 25) ? 1990,11,3 Enter number of days for printout ? 1 OSCAR-13 - G3RUH AMSAT DAY 4689 1990 Nov 3 [Sat] ORBIT: 1828 AP/RAAN: 239/128 ALON/ALAT: 180/0 SAZ/SEL: 210/-72 ILL: 96% UTC MA MODE RANGE EL AZ SQ RR ECL? HGT SLAT SLON ----------------------------------------------------------------------------- 0100 38 B 25929 3 89 48 2.1 vis 20635 13 80 0115 43 B 27716 8 87 43 1.9 vis 22880 17 79 0130 49 B 29345 12 86 38 1.7 vis 24917 21 78 0145 55 B 30825 16 85 34 1.6 vis 26763 24 77 0200 60 B 32160 20 84 30 1.4 vis 28432 26 75 etcAmsat day numbers are reckoned from 0 = 1978 Jan 01; AP is argument of perigee; ALON/ALAT are the satellite's attitude; SAZ/SEL are Sun's position in the orbit plane, and ILL is solar panel illumination. MA is mean anomaly in units of 256 per orbit. SQ is squint angle, RR is range rate (km/s), ECL? will indicate if the satellite is in eclipse, or whether it is potentially visible. HGT is height (km), and SLAT SLON are sub-satellite latitude and longitude (deg East).
PROCinit (lines 1000-1840): All the constants needed by the routines are established here. Most relate to a physical quantity, but are then combined with others or need units changing to form a derived quantity. Some of these constants are only used transiently within "init" itself, but are included for clarity.
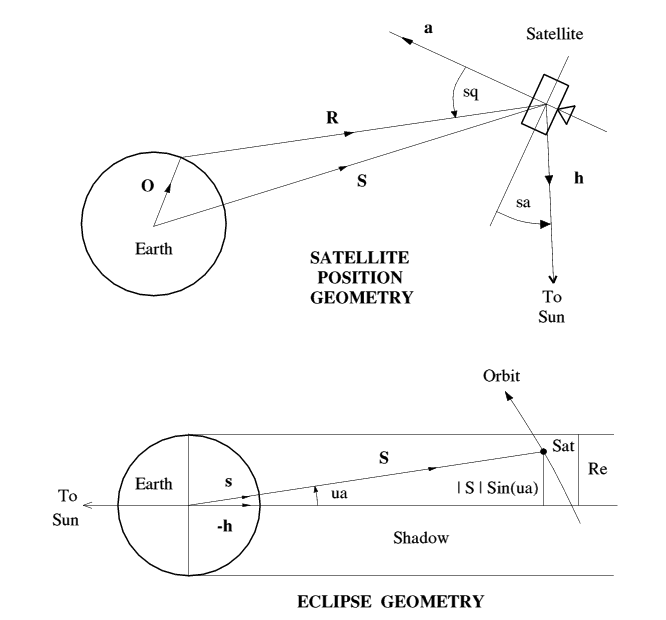
PROCsatvec (lines 2000-2430): Takes input variables day (DN) and fraction of day (TN) and computes satellite position, velocity and antenna direction in orbit plane coordinates. These are then output in celestial coordinates and geocentric coordinates.
PROCrangevec (lines 4000-4200): Calculates Range vector from satellite and observer vector, and derives range, azimuth, elevation, squint, range rate and sub-satellite point.
PROCsunvec (lines 3000-3260): Computes Sun's position in celestial coordinates, and then Sun angle, illumination, visibility and eclipse details. Actual visibility also depends on brightness of satellite, and darkness of sky.
FNday(Y,M,D) Function returns a general day number from year, month and day. Value is Julian Day - 1721409.5 or Amsat day + 722100
FNdate(DN) Function converts day number to a string, e.g. 1990 Nov 3 [Sat]
FNatn(Y,X) Crash-proof four quadrant arctangent. Returns value in range 0-2pi
BBC BASIC Effect OTHER BASICS --------------------------------------------------------------------- PROCname .... ENDPROC subroutine GOSUB nnnn .... RETURN DEG(X) rad -> deg X*180/PI ) where PI = RAD(X) deg -> rad X*PI/180 ) 3.141592654 ASN(X) arcsin FNatn(X,SQR(1-X*X)) ACS(X) arccos PI/2 - FNatn(X,SQR(1-X*X)) ---------------------------------------------------------------------
10 T$="PLAN13": REM OSCAR-13 POSITION, SUN + ECLIPSE PLANNER
20 REM
30 IS$="v2.0": REM Last modified 1990 Aug 12 by JRM
40 REM
50 REM (C)1990 J.R. Miller G3RUH
60 REM
70 REM Proceeds from the sale of this software go directly to the
80 REM Amateur Satellite Programme that helped fund AO-13.
90 REM If you take a copy PLEASE also send a small donation to:
100 REM AMSAT-UK, LONDON, E12 5EQ.
110
120 MODE 3: REM Screen 80 columns
130 PROCinit: REM Set up constants
140
150 INPUT "Enter start date (e.g. 1990, 12, 25) ";YR,MN,DY
160 INPUT "Enter number of days for printout ";ND
170 DS = FNday(YR,MN,DY): REM Start day No.
180 DF = DS + ND - 1: REM Finish day No.
190 FOR DN = DS TO DF
200 FOR HR = 0 TO 23
210 FOR MIN = 0 TO 45 STEP 15
220 TN = (HR+MIN/60)/24
230 PROCsatvec
240 PROCrangevec
250 PROCsunvec
260 IF EL > 0 THEN PROCprintdata
270 NEXT:NEXT:NEXT
280 END
1000 DEF PROCinit
1010 REM SATELLITE EPHEMERIS
1020 REM -------------------
1030 SAT$="OSCAR-13"
1040 YE = 1990 : REM Epoch Year year
1050 TE = 191.145409: REM Epoch time days
1060 IN = 56.9975 : REM Inclination deg
1070 RA = 146.4527 : REM R.A.A.N. deg
1080 EC = 0.6986 : REM Eccentricity -
1090 WP = 231.0027 : REM Arg perigee deg
1100 MA = 43.2637 : REM Mean anomaly deg
1110 MM = 2.09695848: REM Mean motion rev/d
1120 M2 = 1E-8 : REM Decay Rate rev/d/d
1130 RV = 1585 : REM Orbit number -
1140 ALON = 180 : REM Sat attitude, deg. 180 = nominal ) See bulletins
1150 ALAT = 0 : REM Sat attitude, deg. 0 = nominal ) for latest
1160
1170 REM Observer's location + North, + East, ASL(m)
1180 LOC$="G3RUH": LA = 52.21: LO = 0.06: HT = 79: REM Cambridge, UK
1190
1200 LA = RAD(LA): LO = RAD(LO): HT = HT/1000
1210 CL = COS(LA): SL = SIN(LA): CO = COS(LO): SO = SIN(LO)
1220 RE = 6378.137: FL = 1/298.257224: REM WGS-84 Earth ellipsoid
1230 RP = RE*(1-FL): XX = RE*RE: ZZ = RP*RP
1240 D = SQR(XX*CL*CL + ZZ*SL*SL)
1250 Rx = XX/D + HT: Rz = ZZ/D + HT
1260
1270 REM Observer's unit vectors UP EAST and NORTH in GEOCENTRIC coords.
1280 Ux =CL*CO: Ex =-SO: Nx =-SL*CO
1290 Uy =CL*SO: Ey = CO: Ny =-SL*SO
1300 Uz =SL : Ez = 0: Nz = CL
1310
1320 REM Observer's XYZ coords at Earth's surface
1330 Ox = Rx*Ux: Oy = Rx*Uy: Oz = Rz*Uz
1340
1350 REM Convert angles to radians etc.
1360 RA = RAD(RA): IN = RAD(IN): WP = RAD(WP)
1370 MA = RAD(MA): MM = MM*2*PI: M2 = M2*2*PI
1380
1390 YM = 365.25: REM Mean Year, days
1400 YT = 365.2421874: REM Tropical year, days
1410 WW = 2*PI/YT: REM Earth's rotation rate, rads/whole day
1420 WE = 2*PI + WW: REM ditto radians/day
1430 W0 = WE/86400: REM ditto radians/sec
1440
1450 VOx=-Oy*W0: VOy=Ox*W0: REM Observer's velocity, GEOCENTRIC coords. (VOz=0)
1460
1470 REM Convert satellite Epoch to Day No. and Fraction of day
1480 DE = FNday(YE,1,0)+INT(TE): TE = TE-INT(TE)
1490
1500 REM Average Precession rates
1510 GM = 3.986E5: REM Earth's Gravitational constant km^3/s^2
1520 J2 = 1.08263E-3: REM 2nd Zonal coeff, Earth's Gravity Field
1530 N0 = MM/86400: REM Mean motion rad/s
1540 A0 = (GM/N0/N0)^(1/3): REM Semi major axis km
1550 B0 = A0*SQR(1-EC*EC): REM Semi minor axis km
1560 SI = SIN(IN): CI = COS(IN)
1570 PC = RE*A0/(B0*B0): PC = 1.5*J2*PC*PC*MM: REM Precession const, rad/Day
1580 QD = -PC*CI: REM Node precession rate, rad/day
1590 WD = PC*(5*CI*CI-1)/2: REM Perigee precession rate, rad/day
1600 DC = -2*M2/MM/3: REM Drag coeff. (Angular momentum rate)/(Ang mom) s^-1
1610
1615 REM *** Please see end of listing for newer values; use old ones for test. ***
1617
1620 REM Sidereal and Solar data. Rarely needs changing. Valid to year ~2015
1630 YG = 2000: G0 = 98.9821: REM GHAA, Year YG, Jan 0.0
1640 MAS0 = 356.0507: MASD = 0.98560028: REM MA Sun and rate, deg, deg/day
1650 INS = RAD(23.4393): CNS = COS(INS): SNS = SIN(INS): REM Sun's inclination
1660 EQC1=0.03342: EQC2=0.00035: REM Sun's Equation of centre terms
1670
1680 REM Bring Sun data to Satellite Epoch
1690 TEG = (DE-FNday(YG,1,0)) + TE: REM Elapsed Time: Epoch - YG
1700 GHAE = RAD(G0) + TEG*WE: REM GHA Aries, epoch
1710 MRSE = RAD(G0) + TEG*WW + PI: REM Mean RA Sun at Sat epoch
1720 MASE = RAD(MAS0 + MASD*TEG): REM Mean MA Sun ..
1730
1740 REM Antenna unit vector in orbit plane coordinates.
1750 CO=COS(RAD(ALON)): SO=SIN(RAD(ALON))
1760 CL=COS(RAD(ALAT)): SL=SIN(RAD(ALAT))
1770 ax = -CL*CO: ay = -CL*SO: az = -SL
1780
1790 REM Miscellaneous
1800 @%=&507: REM 5 decimals, field 7
1810 OLDRN=-99999
1820 PRINT T$;" ";IS$;" SATELLITE PREDICTIONS"
1830 PRINT STRING$(35,"-")
1840 ENDPROC
2000 DEF PROCsatvec
2010 REM Calculate Satellite Position at DN,TN
2020 T = (DN - DE) + (TN-TE):REM Elapsed T since epoch, days
2030 DT = DC*T/2: KD = 1+4*DT:KDP= 1-7*DT: REM Linear drag terms
2040 M = MA + MM*T*(1-3*DT): REM Mean anomaly at YR,TN
2050 DR = INT(M/(2*PI)): REM Strip out whole no of revs
2060 M = M - DR*2*PI: REM M now in range 0 - 2pi
2070 RN = RV + DR: REM Current Orbit number
2080
2090 REM Solve M = EA - EC*SIN(EA) for EA given M, by Newton's Method
2100 EA = M: REM Initial solution
2110 REPEAT
2120 C = COS(EA): S = SIN(EA): DNOM=1-EC*C
2130 D = (EA-EC*S-M)/DNOM: REM Change to EA for better solution
2140 EA = EA - D: REM by this amount
2150 UNTIL ABS(D) < 1E-5: REM Until converged
2160
2170 A = A0*KD: B = B0*KD: RS = A*DNOM: REM Distances
2180
2190 REM Calc satellite position & velocity in plane of ellipse
2200 Sx = A*(C-EC): Vx=-A*S/DNOM*N0
2210 Sy = B*S: Vy= B*C/DNOM*N0
2220
2230 AP = WP + WD*T*KDP: CW = COS(AP): SW = SIN(AP)
2240 RAAN = RA + QD*T*KDP: CQ = COS(RAAN): SQ = SIN(RAAN)
2250
2260 REM Plane -> celestial coordinate transformation, [C] = [RAAN]*[IN]*[AP]
2270 CXx=CW*CQ-SW*CI*SQ: CXy=-SW*CQ-CW*CI*SQ: CXz= SI*SQ
2280 CYx=CW*SQ+SW*CI*CQ: CYy=-SW*SQ+CW*CI*CQ: CYz=-SI*CQ
2290 CZx=SW*SI: CZy= CW*SI: CZz= CI
2300
2310 REM Compute SATellite's position vector, ANTenna axis unit vector
2320 REM and VELocity in CELESTIAL coordinates. (Note: Sz=0, Vz=0)
2330 SATx=Sx*CXx+Sy*CXy: ANTx=ax*CXx+ay*CXy+az*CXz: VELx=Vx*CXx+Vy*CXy
2340 SATy=Sx*CYx+Sy*CYy: ANTy=ax*CYx+ay*CYy+az*CYz: VELy=Vx*CYx+Vy*CYy
2350 SATz=Sx*CZx+Sy*CZy: ANTz=ax*CZx+ay*CZy+az*CZz: VELz=Vx*CZx+Vy*CZy
2360
2370 REM Also express SAT,ANT and VEL in GEOCENTRIC coordinates:
2380 GHAA = GHAE + WE*T: REM GHA Aries at elapsed time T
2390 C = COS(-GHAA): S = SIN(-GHAA)
2400 Sx=SATx*C - SATy*S: Ax=ANTx*C - ANTy*S: Vx=VELx*C - VELy*S
2410 Sy=SATx*S + SATy*C: Ay=ANTx*S + ANTy*C: Vy=VELx*S + VELy*C
2420 Sz=SATz: Az=ANTz: Vz=VELz
2430 ENDPROC
3000 DEF PROCsunvec
3010 MAS = MASE + RAD(MASD*T): REM MA of Sun round its orbit
3020 TAS = MRSE + WW*T + EQC1*SIN(MAS) + EQC2*SIN(2*MAS)
3030 C = COS(TAS): S=SIN(TAS): REM Sin/Cos Sun's true anomaly
3040 SUNx=C: SUNy=S*CNS: SUNz=S*SNS: REM Sun unit vector - CELESTIAL coords
3050
3060 REM Find Solar angle, illumination, and eclipse status.
3070 SSA = -(ANTx*SUNx + ANTy*SUNy + ANTz*SUNz):REM Sin of Sun angle -a.h
3080 ILL = SQR(1-SSA*SSA): REM Illumination
3090 CUA = -(SATx*SUNx+SATy*SUNy+SATz*SUNz)/RS: REM Cos of umbral angle -h.s
3100 UMD = RS*SQR(1-CUA*CUA)/RE: REM Umbral dist, Earth radii
3110 IF CUA>=0 THEN ECL$=" +" ELSE ECL$=" -": REM + for shadow side
3120 IF UMD <= 1 AND CUA>=0 THEN ECL$=" ECL": REM - for sunny side
3130
3140 REM Obtain SUN unit vector in GEOCENTRIC coordinates
3150 C = COS(-GHAA): S = SIN(-GHAA)
3160 Hx=SUNx*C - SUNy*S
3170 Hy=SUNx*S + SUNy*C: REM If Sun more than 10 deg below horizon
3180 Hz=SUNz: REM satellite possibly visible
3190 IF (Hx*Ux+Hy*Uy+Hz*Uz < -0.17) AND (ECL$ <> " ECL") THEN ECL$=" vis"
3200
3210 REM Obtain Sun unit vector in ORBIT coordinates
3220 Hx = SUNx*CXx + SUNy*CYx + SUNz*CZx
3230 Hy = SUNx*CXy + SUNy*CYy + SUNz*CZy
3240 Hz = SUNx*CXz + SUNy*CYz + SUNz*CZz
3250 SEL = ASN(Hz): SAZ= FNatn(Hy,Hx)
3260 ENDPROC
4000 DEF PROCrangevec
4010 REM Compute and manipulate range/velocity/antenna vectors
4020 Rx = Sx-Ox: Ry = Sy-Oy: Rz = Sz-Oz: REM Rangevec = Satvec - Obsvec
4030 R = SQR(Rx*Rx+Ry*Ry+Rz*Rz): REM Range magnitude
4040 Rx=Rx/R: Ry=Ry/R: Rz=Rz/R: REM Normalise Range vector
4050 U = Rx*Ux+Ry*Uy+Rz*Uz: REM UP Component of unit range
4060 E = Rx*Ex+Ry*Ey: REM EAST do (Ez=0)
4070 N = Rx*Nx+Ry*Ny+Rz*Nz: REM NORTH do
4080 AZ = DEG(FNatn(E,N)): REM Azimuth
4090 EL = DEG(ASN(U)): REM Elevation
4100
4110 REM Resolve antenna vector along unit range vector, -r.a = Cos(SQ)
4120 SQ = DEG(ACS(-(Ax*Rx + Ay*Ry + Az*Rz))): REM Hi-gain ant SQuint
4130
4140 REM Calculate sub-satellite Lat/Lon
4150 SLON = DEG(FNatn(Sy,Sx)): REM Lon, + East
4160 SLAT = DEG(ASN(Sz/RS)): REM Lat, + North
4170
4180 REM Resolve Sat-Obs velocity vector along unit range vector. (VOz=0)
4190 RR = (Vx-VOx)*Rx + (Vy-VOy)*Ry + Vz*Rz: REM Range rate, km/s
4200 ENDPROC
4220 DEF FNatn(Y,X)
4230 IF X <> 0 THEN A=ATN(Y/X) ELSE A=PI/2*SGN(Y)
4240 IF X < 0 THEN A=A+PI
4250 IF A < 0 THEN A=A+2*PI
4260 =A
4280 DEF PROCmode
4290 M=INT(M*128/PI)
4300 REM Mode switching MA/256
4310 MD$="-"
4320 IF M >= 0 THEN MD$="B"
4330 IF M >= 100 THEN MD$="L"
4340 IF M >= 130 THEN MD$="S"
4350 IF M >= 135 THEN MD$="B"
4360 IF M >= 220 THEN MD$="-"
4370 ENDPROC
5000 DEF FNdate(D)
5010 REM Convert day-number to date; valid 1900 Mar 01 - 2100 Feb 28
5020 D=D+428: DW=(D+5)MOD7
5030 Y=INT((D-122.1)/YM): D=D-INT(Y*YM)
5040 MN=INT(D/30.61): D=D-INT(MN*30.6)
5050 MN=MN-1: IF MN>12 THEN MN=MN-12: Y=Y+1
5060 D$=STR$(Y)+" "+MID$("JanFebMarAprMayJunJulAugSepOctNovDec",3*MN-2,3)
5070 =D$+" "+STR$(D)+" ["+MID$("SunMonTueWedThuFriSat",3*DW+1,3)+"]"
5080
5090 DEF FNday(Y,M,D)
5100 REM Convert date to day-number
5110 IF M<=2 THEN Y=Y-1: M=M+12
5120 =INT(Y*YM) + INT((M+1)*30.6) + D-428
6000 DEF PROCprintdata
6010 REM Construct time as a string
6020 HR$=STR$(HR): MIN$=STR$(MIN)
6030 IF LEN(HR$) < 2 THEN HR$="0"+HR$
6040 IF LEN(MIN$) < 2 THEN MIN$="0"+MIN$
6050 TIM$=HR$+MIN$+" "
6060
6070 PROCmode: REM Get AO-13 mode. Now round-off data
6080 R=FNrn(R): EL=FNrn(EL): AZ=FNrn(AZ): SQ=FNrn(SQ): RR=FNrn(RR*10)/10
6090 HGT=FNrn(RS-RE): SLON=FNrn(SLON): SLAT=FNrn(SLAT)
6100 IF RN <> OLDRN THEN OLDRN=RN: PROCheader
6110 PRINT TIM$;STR$(M);" ";MD$,R,EL,AZ,SQ,RR,ECL$,HGT,SLAT,SLON
6120 ENDPROC
6130
6140 DEF PROCheader
6150 RAAN=FNrn(DEG(RAAN)): AP=FNrn(DEG(AP)): SAZ=FNrn(DEG(SAZ))
6160 SEL=FNrn(DEG(SEL)): ILL=FNrn(100*ILL)
6170 PRINT: PRINT
6180 PRINT SAT$;" - "LOC$;SPC(16);"AMSAT DAY ";STR$(DN-722100);SPC(12);FNdate(DN)
6190 PRINT "ORBIT: ";RN;" AP/RAAN: ";AP;"/";RAAN;" ALON/ALAT:";ALON;"/";ALAT;
6200 PRINT" SAZ/SEL: ";SAZ;"/";SEL;" ILL: ";ILL;"%"
6210 PRINT
6220 PRINT " UTC MA MODE RANGE EL AZ SQ RR ECL? ";
6230 PRINT "HGT SLAT SLON"
6240 PRINT STRING$(77,"-")
6250 ENDPROC
6260
6270 DEF FNrn(X) = INT(X+0.5)
*** Astronomical data for 2023 onwards
�1620�REM�Sidereal�and�Solar�data.
�1630�YG�=�2023:�G0�=�99.4057:��REM�GHAA,�Year�YG,�Jan�0.0
�1640�MAS0�=�356.0787:�MASD�=�0.98560028:�REM�MA�Sun�and�rate,�deg,�deg/day
�1650�INS�=�RAD(23.4363):�CNS�=�COS(INS):�SNS�=�SIN(INS):�REM�Sun's�inclination
�1660�EQC1=0.03340:�EQC2=0.00035:���REM�Sun's�Equation�of�centre�terms
***
In earlier versions of the program, the conversion of a vector from Orbit plane coordinates to Celestial coordinates was written out stage by stage. That is, a rotation in argument of perigee, followed by a rotation through inclination, and finally through RAAN. Since there are actually several vectors (satellite position, velocity and antenna axis) to transform, this became a little clumsy, so the three rotations are now amalgamated into one. The array [C] that does this is computed at lines 2260-2290.
Celestial -> Orbit Plane Coordinate Transformation
The array [C] can also be used in the reverse direction, to convert a vector from Celestial to Orbit plane coordinates. This is done by "transposing the array", using C(J,I) for C(I,J) throughout. This is used to calculate the Sun's position as seen from the orbit plane (lines 3210-3240).
Decay
The Keplerian element DECAY is half the rate of change of mean motion. DECAY is usually very small, of order 10^-7, and its short term influence is small. For example, MA is affected by an amount DECAY*T*T over T days. Over 100 days that makes 10^-7*100*100 = 0.001 revolutions, or about 7.2 seconds for a 2 hour period satellite.
Decay is only really significant for low altitude satellites such as the space shuttle, ISS, or satellites nearing burn-up. Then the value can be as large as 10^-4. This causes in addition a noticeable second order effect on semi-major axis, argument of perigee and RAAN. The program accounts for this with terms calculated at line 2030.
For many purposes, especially if the Keplerian elements are regularly updated, drag can be ignored. This is true in particular for Oscar-13, where the unmodelled luni-solar perturbations are substantially larger than "decay".
Doppler Shift
The program calculates range-rate RR (line 4190) in km/s. If a satellite transmits a frequency FT, then this is received as a frequency FR:
FR = FT * (1 - RR/299792). [Note: 299792 is the speed of light in km/s]
Thus the "doppler shift" FD is given by: FD = -FT*RR/299792.
The calculation of range-rate is accurate in vacuo. However, at low elevations the radio path through the Earth's atmosphere is not perfectly straight. This refraction causes the actual observed doppler shift at AOS and LOS to be as much as 1 part in 10^7 in error, say 50-100 Hz at 435 MHz. It should also be noted that simple crystal oscillators have a similar order of stability, and satellites usually experience large temperature changes.
Footprint
In some programs there is a requirement to draw a circle around the sub- satellite point to indicate the field of view of the satellite. The following routine indicates how to do this. It is coded for clarity, not for speed. It would be better to store SIN(A) and COS(A) in a table rather than compute them every call. Since the footprint is left-right symmetric, only one half of the circle's points need be computed, and the other half can be inferred logically.
The sub-routine's output is a unit vector {X,Y,Z} in geocentric coordinates for the I'th point on the Earth's surface. This will then need transforming to map coordinates (mercator, spherical, linear or whatever), and then screen coordinates to suit the computer.
DEF PROCfoot(RS, slat, slon) REM Take satellite distance, sub-satellite lat/lon and compute unit vectors' REM x,y,z of N points of footprint on Earth's surface in Geocentric REM Coordinates. Also terrestrial latitude and longitude of points. : srad = ACS(RE/RS): REM Radius of footprint circle cla = COS(slat): sla = SIN(slat): REM Sin/Cos these to save time clo = COS(slon): slo = SIN(slon) sra = SIN(srad): cra = COS(srad) FOR I = 0 TO N: REM N points to the circle A = 2*PI*I/N: REM Angle around the circle : X = cra: REM Circle of points centred on Lat=0, Lon=0 Y = sra*SIN(A): REM assuming Earth's radius = 1 Z = sra*COS(A) REM [ However, use a table for SIN(.) COS(.) ] : x = X*cla - Z*sla: REM Rotate point "up" by latitude slat y = Y z = X*sla + Z*cla : X = x*clo - y*slo: REM Rotate point "around" through longitude slon Y = x*slo + y*clo Z = z : LON(I) = FNatn(Y,X): REM Convert point to Lat/Lon (or as required by map LAT(I) = ASN(Z): REM projection and display system). NEXT I ENDPROC
Squint Angle
Squint (or pointing) angle is the angle between the spacecraft's antenna and the observer. This is calculated at line 4120 for Oscar-13's high-gain antennas. As the low gain antennas are simple monopoles radiating normal to the a axis, low-gain squint is given by:
SQ_low_gain = 90 - SQ_high_gain (deg)Some satellites are stabilised so that they are continuously Earth pointing (e. g. UOSATs). For these, the antenna axis unit vector is aligned with the spacecraft's position vector, i.e. a = -s So to calculate the squint angle for these satellites use the formula:
4120 SQ = DEG(ACS( (Sx*Rx + Sy*Ry + SZ*Rz)/RS )) (deg)Sun Model and Sidereal Constants
The calculations of Earth rotation and Sun position are the most accurate part of this program! There is no need to update the solar constants at lines 1630-1660 for several decades.
This program was written and evolved over a period of years from 1983 to 1990. Constructive comment and suggestions are welcome.
Feedback on these pages to Webmaster. Feedback on the article should be sent to James Miller
Created: 1994 Dec 09 -- Last modified: 2023 Apr 12